News

Creativity and the discovery of new ideas and concepts are fascinating and mysterious processes. To shed light on the mechanisms behind them, mathematicians study such exploration processes as time-ordered sequences of events, like the songs listened to by an individual or the titles of scientific publications. A "discovery" or "novelty" is usually described to happen when a certain event occurs for the first time, e.g., the first time a song by a particular artist is played or the first time a scientific article mentions a certain keyword.

In a recent study published in Nature Communications, a team around Professor Vito Latora and his former PhD student Gabriele Di Bona from the Centre for Complex Systems turned to the importance of studying higher-order connections in these processes: New ideas often do not appear out of the blue, but through the combination of previously known concepts. Instead of looking at individual elements in event sequences, the team thus investigated how novel transitions between two or more events emerge. They could confirm that the frequency of such "higher-order novelties" can be described by similar mathematical relations as previously studied first-order novelties, but the quantitative details can be different. Notably, the inclusion of higher-order effects allows them to distinguish processes that exhibited similar characteristics at first order.

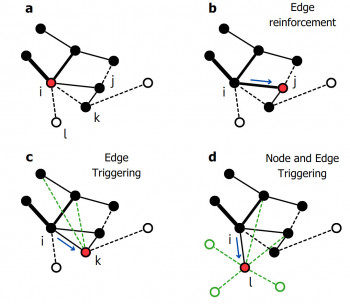
The researchers also devised a mathematical network model for these exploration processes that captures the phenomenology observed in real-world data. Events are represented by the network's nodes, and exploration is modeled by a walker wandering along the network's edges. A discovery happens whenever the walker visits a node ("first-order novelty") or uses an edge ("second-order novelty") for the first time. This also triggers the creation of new nodes and edges, modeling how discoveries unlock new possibilities. As illustrated in the figure at the top, it results in an ever growing and evolving network of concepts and events.

It will be exciting to watch where the researchers' own exploration process of the science behind discovery takes them next ...

See also:

• the original research article: G. Di Bona et al., The dynamics of higher-order novelties, Nat. Commun. 16, 393 (2025)
• coverage on phys.org: Tejasri Gururaj, Scientists map the mathematics behind how we create and innovate, phys.org, 29 January 2025