Analysis and PDE Theory

Linear and nonlinear partial differential equations (PDEs) arise in basically all sciences (physics, chemistry, medicine, engineering, astronomy, etc). In Physics, hyperbolic PDES model several important phenomena, from propagation of waves in a medium (for instance propagation of seismic waves during an earthquake) to refraction in crystals and gas-dynamics.

In the Centre we have experts of hyperbolic equations and systems with multiplicities who employ pseudo- and Fourier integral operator methods to prove the well-posedness of the corresponding Cauchy problem in suitable function spaces. Their research involves microlocal analysis as well as regularisation methods to provide very weak solutions in case of highly singular coefficients.

Sub-elliptic problems are also investigated in the context of Lie groups. Important problems in the realm of PDEs are unique continuation and control theory. The problem of unique continuation in PDEs asks whether a solution is fully determined by its data imposed on a smaller area. Such questions have been studied using a wide range of tools (e.g. microlocal analysis, geometric methods), and have found a large variety of applications, for instance in control theory and inverse problems. The control theory of PDEs is concerned with whether solutions to a PDE can be forced to behave in a desired manner through some limit inputs, or controls. Moreover, control theory is connected to many important problems in engineering, science, and mathematics.

In the Centre, we also have experts in the control theory of various hyperbolic and parabolic equations.

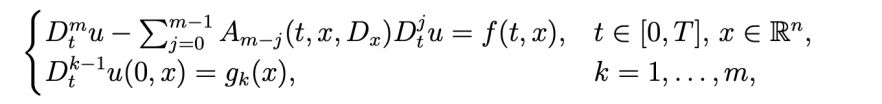
Cauchy problem for m-order hyperbolic equations