Optimum Sensor Placement

Dr Ward has worked with PA Consulting and DSTL to develop optimisation methods for placing electromagnetic sensors in urban environments. Suppose that there is a malicious transmitter located somewhere within a city. We can observe the action of this transmitter via various types of sensors that can measure signal strength, time difference of arrival, direction, etc. and want to use this data to rapidly identify its location. Of course, we do not know in advance where the transmitter may appear, so how should we select and place our sensors so that they give a reasonable localisation in all potential scenarios? Will Handley (Cambridge) and Dr Ward developed a small, simulated “forward model" for EM propagation in urban environments and then used 2 methods, which apply nested sampling and mixed-integer linear programming, respectively, to answer this question.

This work came about from Dr Ward’s participation in the “Challenges in the Electromagnetic Environment” workshop series (1, 2, 3), sponsored by DSTL and PA Consulting, hosted by the Isaac Newton Institute. The work was presented as one of the workshop’s “Success Stories” at the meeting held on July 29, 2021, and received another round of funding from DSTL and PA consulting for follow-on work.
 
Dr Ward has also since been invited and attended the “Limits of EMA” Workshop held at PA Consulting on 11–13 January 2022 and the Mathematical Challenges in Defence and Security Workshop held at the INI on 15–16 March 2023. This last workshop has resulted in the submission of a joint bid to DSTL for funding to carry out work on optimising resources for detection of objects in space.

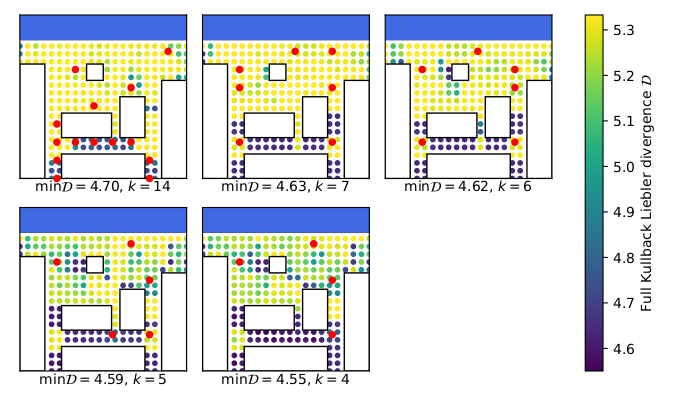
Optimal sensor placements for various reductions in uncertainty in the discrete model

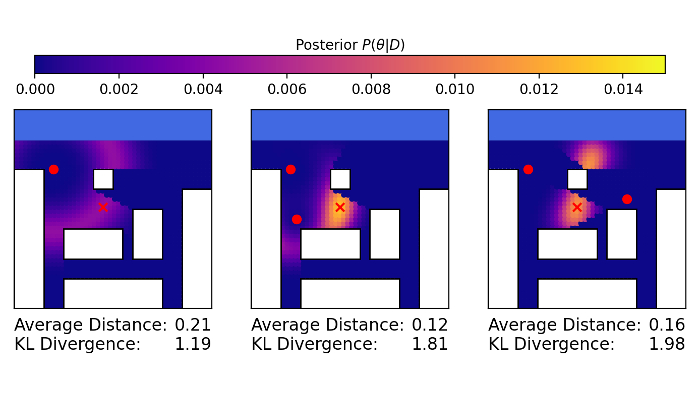
Comparison of objective functions: KL-divergence from the prior measures information gain while average distance measures the expected localisation error in the posterior